Page Contents
Sin(us) Cos(inus)
Sin, Cos movement
The sin() and cos() functions are some of the most used Expressions to create movements. Most likely, you are already familiar with what they do, but in a nutshell, they get a seed value and output a number between -1 and +1. Most often the seed value will be time. As we have learned before, time will simply tell us the current frame number.
Let’s look at the most basic example:
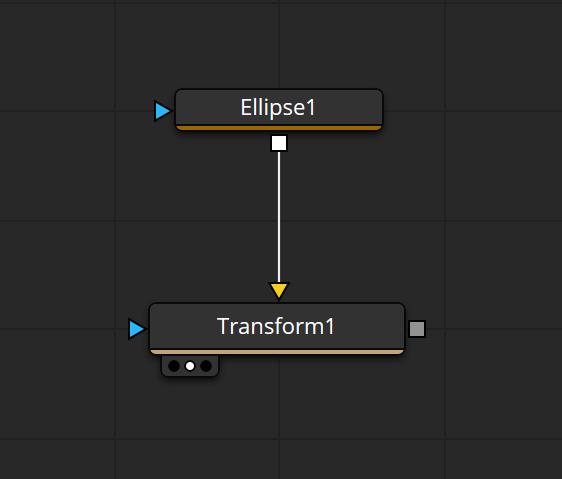
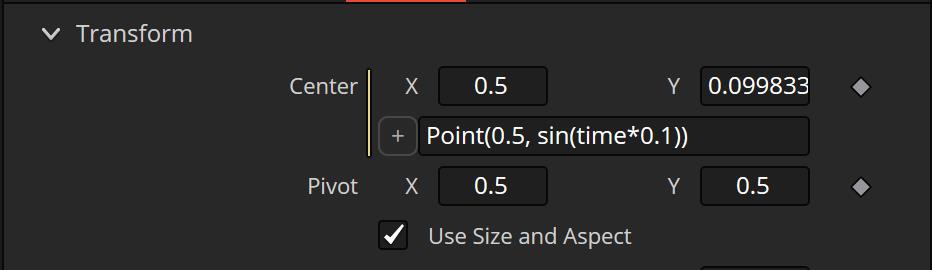
Point(0.5, sin(time*0.1))
Now the Ellipse will move upwards and downwards between -1 and 1. I have multiplied the time by 0.1 so it’s slower. You can also pair this with a custom control to make this more interactive.
But this is problematic because the sphere is gone for much of the animation, because the bottom edge of the coordinate system is 0 and it travels to -1. Let’s change the Expression to this:
Point(0.5, sin(time*0.1)*0.5+0.5)
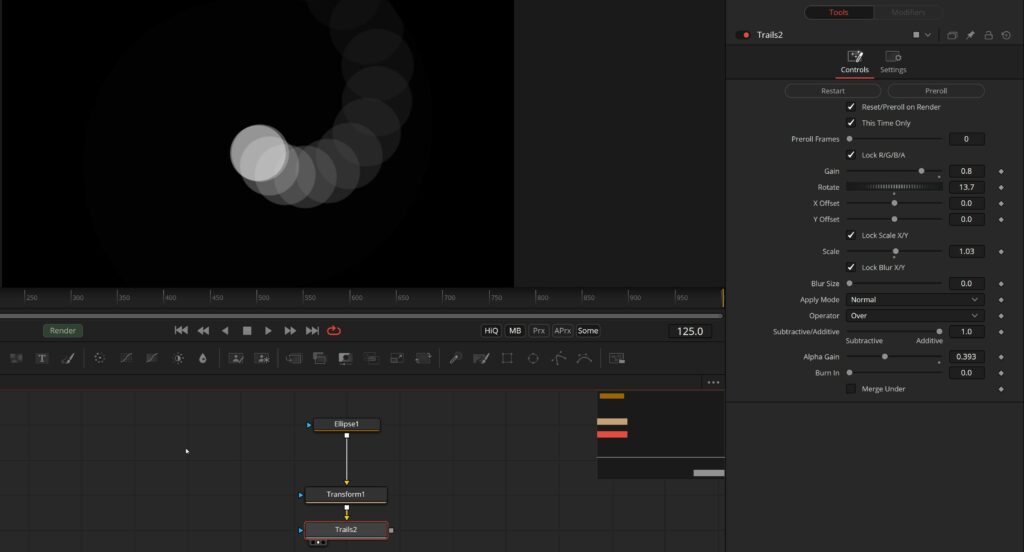
Perfect, now it stays within the limits because then the distance is halved and brought up. Just using this and a Trails tool can already get you some cool graphics.
cos() will do exactly the same except it starts at a different point. You can see the difference by simply replacing sin with cos in the expression.
Circular movement using sin() and cos()
But as we all know, a straight line is boring, circular movement is where it’s at! Luckily for us, sin() on the Y-Axis and cos() and the X-Axis will create a circle.
The expression will look like this:
Point(cos(time*0.1)*0.5+0.5, sin(time*0.1)*0.5+0.5)
As you can see, it’s really just the same on the X-Axis except I switched sin for cos.

But now you might say, “This is an egg, not a circle”. And you are correct, due to Fusion’s relative coordinate system the aspect of the circle will be determined by your resolution. The simple fix is to change the resolution on the ellipse to a square aspect. To this on the Image Tab of the Ellipse tool.
You can also use the Transform tool after the Ellipse to scale it down or reduce the 0.5 multiplier in the Expression to something smaller, so it doesn’t touch the edges.
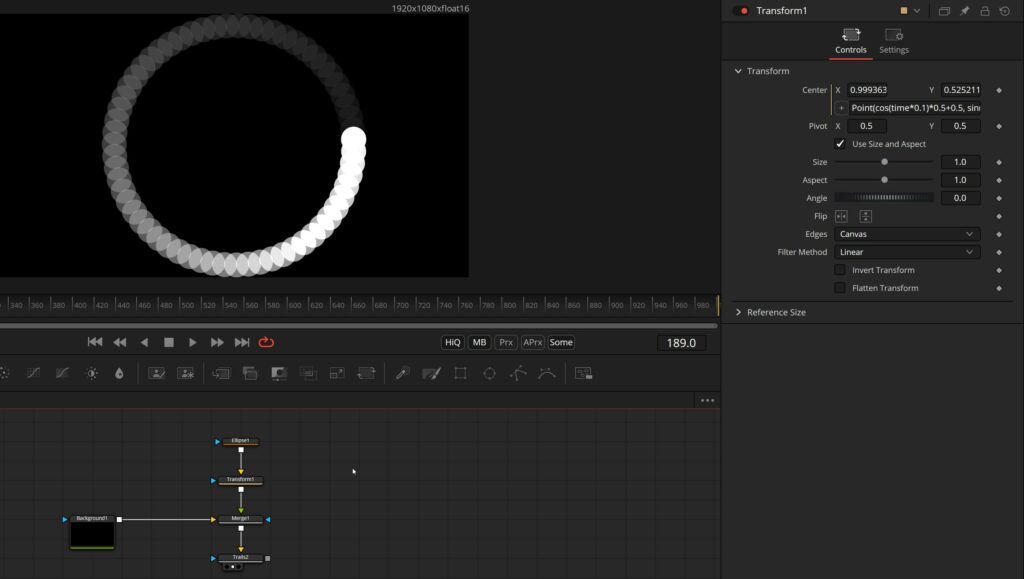
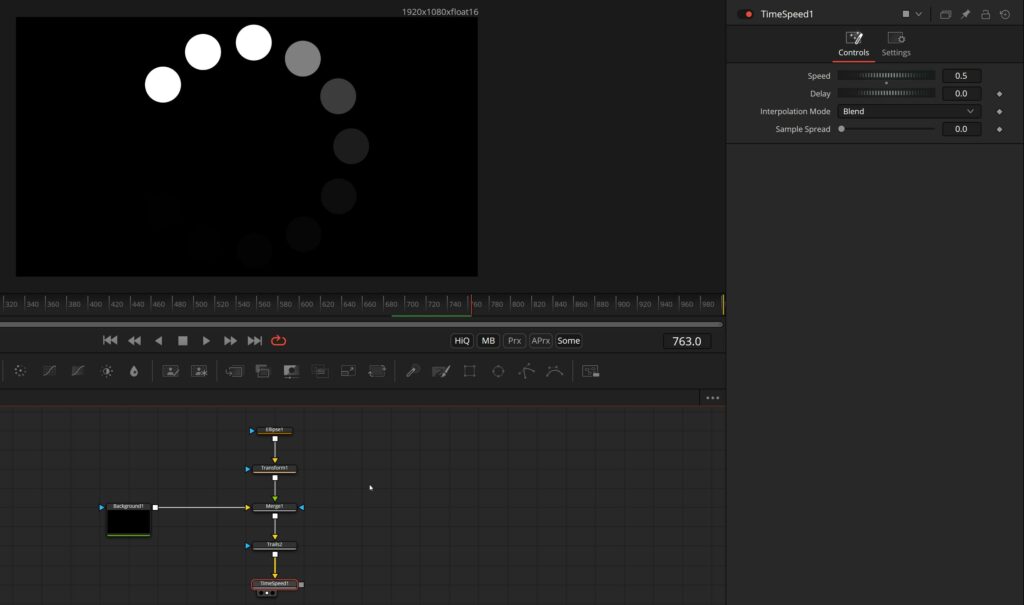
Increase the speed of the sin and cos, add a Timespeed tool to slow it down and you’ve got yourself a great loading or buffering animation:
sin() in a Custom tool
Of course, what’s possible in an Expression can be used in a Custom tool, too. It’s also cool to visualize sin().
Just adding the simple Expression:
c1*sin(x*n1*time)
into the color channels of the custom tool will give us these trippy lines that get smaller and smaller:
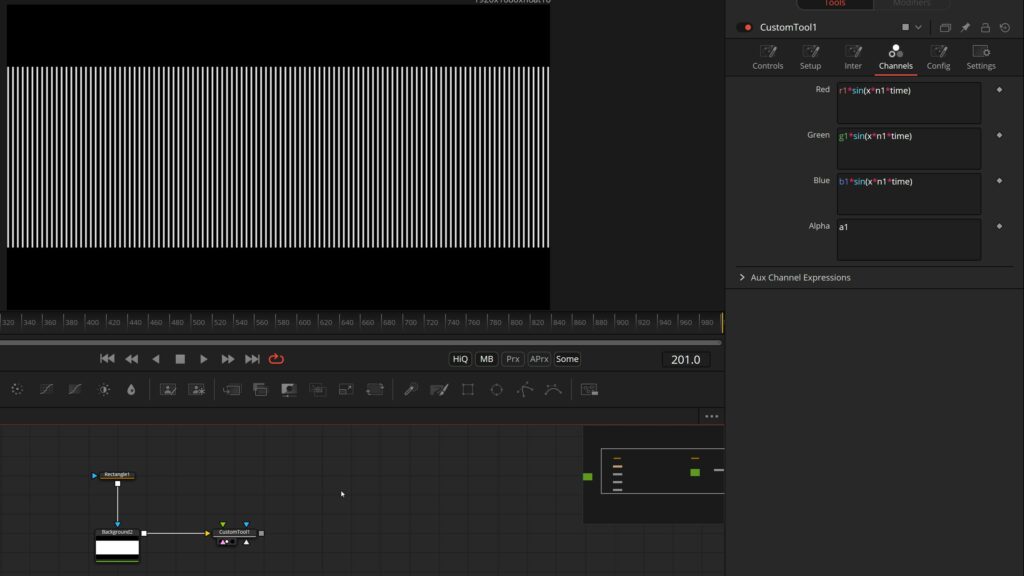
n1 is the first number control on the custom tool and can be used to change the frequency/speed.
If we don’t want them to get smaller over time we can add the seed instead of multiplying:
c1*sin(x*n1+time*n2)
n1 changes frequency, n2 the speed. You probably need very high numbers to see differences. Now we get something like this:
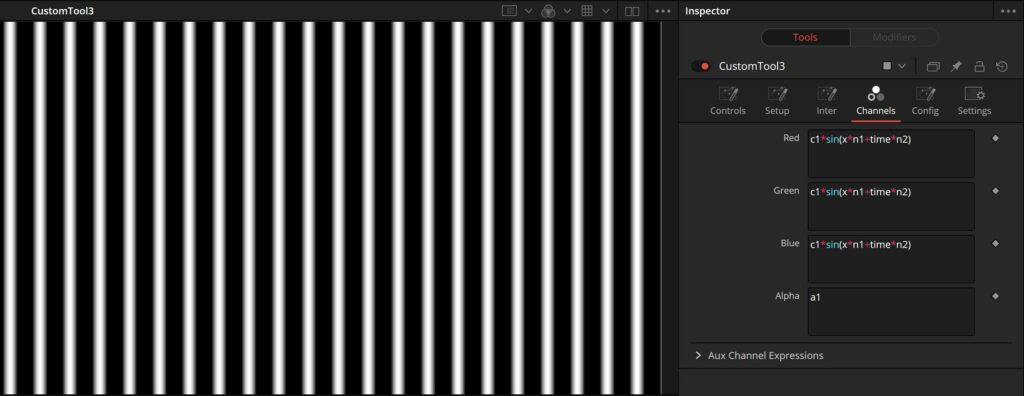
And if we feed this into the second input of a Displace tool, we can get actual sinus waves, or simply displace our image in a sinus pattern:
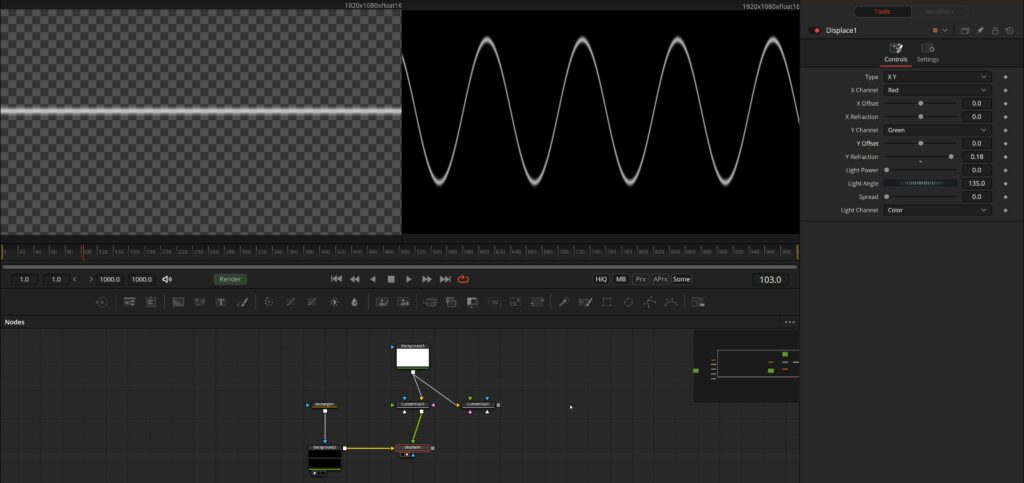
Now, this was quite a long blog post and if you’ve read everything, amazing! You will know more about Expressions than most people. Some parts of this post are a little crunched and shorter in explanation as I usually like, but this post was in my drafts for several months now and needed to be published at some point.
Hopefully, this was useful to you and I will update this post if I find the time and more Expressions to cover.